MATHS ET ART : A PARTIR D’UNE OEUVRE, CONICAL INTERSECT - GORDON MATTA CLARK

La vidéo "Conical Intersect" de Gordon Matta Clark vous a permis de découvrir comment un artiste contemporain s’approprie un domaine des mathématiques : les coniques.

Gordon matta clark par Iconographe

En découpant des sections dans les murs d’une maison vouée à la destruction (quartier du centre Georges Pompidou dans les années 70), Gordon Matta Clark crée une œuvre éphémère où des formes géométriques pures (cercles, ellipses) surgissent d’un univers confus (la maison en ruine, les ouvriers au travail, la poussière, les machines ...). De ce chaos, la destruction, surgit pourtant la beauté.

Nous profitons de cette étude pour aborder un domaine particulier des mathématiques : les coniques.

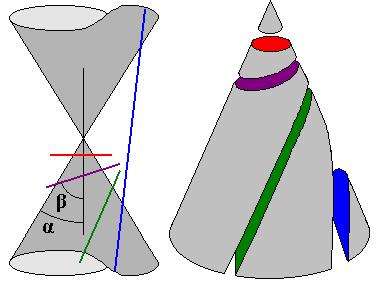
A partir de la figure ci-jointe vous pouvez comprendre comment on forme les coniques par intersection d’un plan et d’un cône (source Wikipédia)

On y retrouve en effet toutes les coniques qu’on peut créer :
– en rouge, des cercles (conique que vous connaissez déjà !)
– en violet, des ellipses
– en vert, des paraboles,
– en bleu, des hyperboles

Nous allons nous intéresser particulièrement aux ellipses.

En voici une définition :

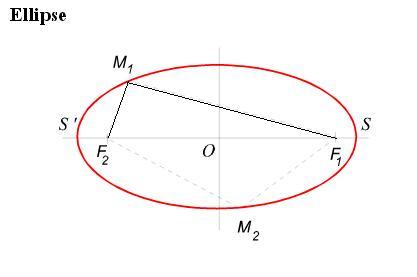
(Source : www.aix-planetarium.fr/ficimages/Coniques.pdf‎)

Vous remarquez à partir de cette définition que si F1=F2=O, l’ellipse ainsi définie est un cercle.

Votre travail en MPS va consister, à partir d’une page automatisée de calculs, sur un tableur, à obtenir des cercles et des ellipses ... mais cela n’est peut-être pas si simple ... et cela nous poussera peut-être à envisager l’utilisation d’autres logiciels ...

Tout d’abord on se reporte à la page du tableur donnée que vous allez compléter :

Remarquez que la première figure qu’on souhaite obtenir, en prenant a=b=3 est un cercle dont vous définirez le centre et le rayon.

Qu’observez-vous à l’écran ? Comment remédier à la difficulté ?

Modifiez les paramètres de a et b afin d’essayer d’obtenir une ellipse ...

On rencontre des difficultés d’échelles sur les représentations graphiques obtenues, alors même que la propriété suivante qui donne l’équation cartésienne d’une ellipse valide notre démarche :

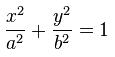
Et cela nous entraine vers "géogébra" pour affiner nos tracés et dessiner nos ellipses.

On complète alors la page "géogébra" en définissant un point M de coordonnées (a.cos(t), b.sin(t)), puis à l’aide du mode trace on obtient des tracés de cercles et d’ellipses ...

Double-cliquez sur la figure ci-dessous :
<geogebra|doc=1772|barre_menu=yes|barre_outils=go|fenetre_externe=oui>

Sur ce logiciel vous pouvez maintenant à partir de chaque ellipse définie par son équation cartésienne, obtenir son tracé géométrique en retrouvant ses foyers F1 et F2.

A vous maintenant de créer une belle galerie de cercles et d’ellipses ... à publier sur votre ENT (évidemment !)

Un grand merci au FRAC Ile de France, qui nous a prêté une copie de la vidéo de Gordon Matta Clark, pour faire découvrir l’œuvre de cet artiste, en classe, dans de bonnes conditions.